Machine Learning: construindo meu primeiro modelo

No artigo anterior, Machine Learning, a tecnologia que está impulsionando a inovação, falamos um pouco sobre o que é Machine Learning e apresentamos as diferentes categorias de algoritmos, bem como os algoritmos mais comuns de cada uma delas. Vimos que os algoritmos de regressão são um dos tipos mais comuns dentro do Aprendizado Supervisionado, e que a forma mais simples deles é a regressão linear. Por conta da simplicidade desse tipo de algoritmo, muitas vezes este é o primeiro que temos contato ao estudar machine learning. Comigo não foi diferente, e vou compartilhar com vocês o caminho que trilhei até conseguir implementar meu primeiro modelo de machine learning!

O que precisamos para seguir nessa trilha?

Para me acompanhar nesse processo você precisa de só uma coisa: vontade de aprender! Eu sei que é um clichê, mas é isso mesmo. É claro que um pouco de conhecimento de álgebra linear e cálculo vai te ajudar bastante na hora de entender a teoria por trás do método, mas o importante é ter a intuição do que o método faz para que você seja capaz de identificar qual é o mais adequado para resolver o seu problema.

Dito isso, meu objetivo é passar para vocês essa intuição, passando por cima dos detalhes técnicos. Então, se quiserem saber mais sobre a teoria, vocês podem entrar em contato comigo e eu, como um amante da matemática que sou, vou responder em detalhes para vocês!

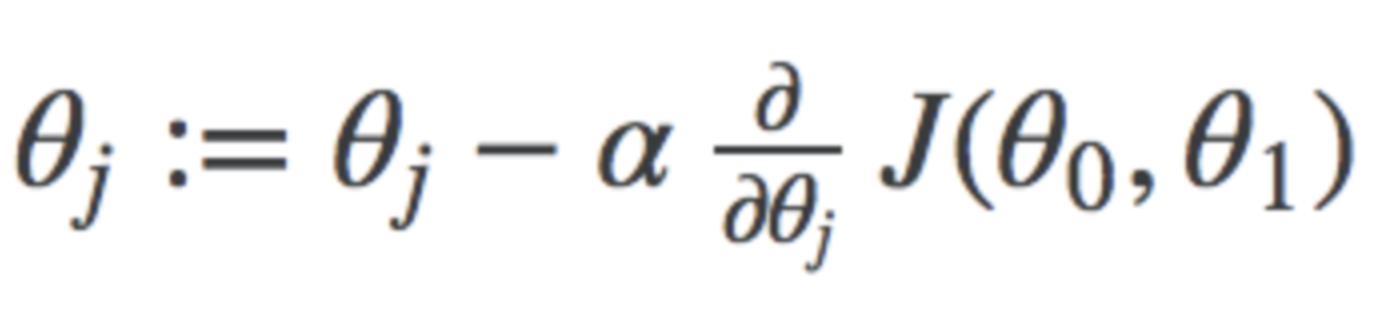
Para os que ficaram curiosos, é precisamente essa parte que eu vou passar por cima.

Para implementar o algoritmo eu decidi usar o Octave, pois ele é um software matemático poderoso e gratuito. Por ser um software matemático, o Octave possui as mais importantes funções e operações matemáticas já programadas nele, nos poupando o trabalho de procurar, aprender e importar várias bibliotecas para que possamos implementar algumas operações matriciais simples. Se você quiser acompanhar a implementação ou treinar o modelo você mesmo, o Octave pode ser baixado por aqui, basta selecionar o instalador da opção recomendada. Para quem é usuário Windows, tem um tutorial rápido, porém em inglês, da instalação do Octave em todas suas versões (exe ou zip) aqui, na Wiki deles.

Também é importante ressaltar que as linguagens mais usadas para machine learning são Python, R, JavaScript, Scala e Matlab/Octave. Como eu disse anteriormente, Octave é um software matemático e, por conta disso, mais usado na área acadêmica. Python provavelmente é a linguagem de programação mais utilizada para machine learning e, caso você queira aprender mais, eu encorajo que você pesquise mais sobre ela.

Finalmente, Regressão Linear

Se você leu o primeiro artigo, você deve se lembrar que a regressão linear é usada para aproximar um conjunto de pontos por uma reta. Uma maneira de medir o quão boa é essa aproximação, é calculando a distância média entre a reta do modelo e os pontos do conjunto, ou o erro da aproximação. A maneira mais usual de calcular esse erro de aproximação é através do erro quadrático médio, que não mais é do que a soma do quadrado das distâncias entre a reta estimada e os valores reais, do conjunto de pontos.

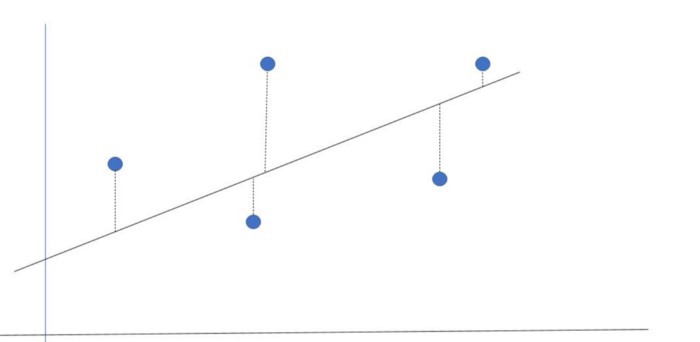
A distância entre o ponto e a reta é o erro da aproximação.

O mais importante dessa maneira de estimar o erro é o fato de que ele é quadrático! Funções quadráticas possuem um formato muito específico, com propriedades muito boas quando o assunto é maximizar ou minimizar o seu valor. Como nosso objetivo é fazer a reta aproximar o conjunto de pontos da melhor maneira possível, nós queremos minimizar esse erro. É aí que entra o método que vamos usar para a regressão linear: a Descida Gradiente.

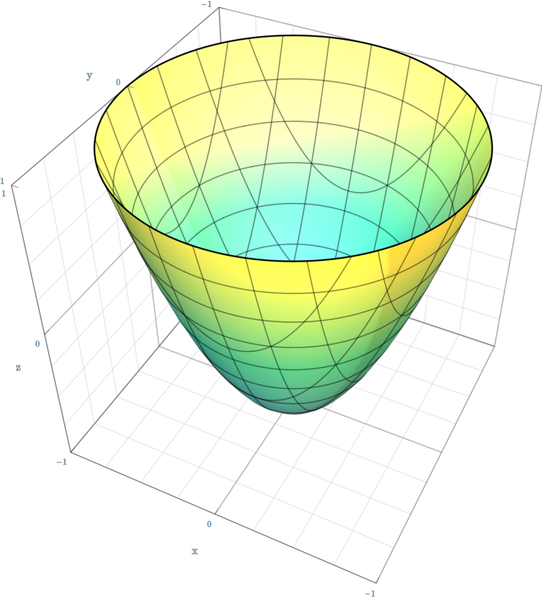
Essa é a figura formada por uma função quadrática, um parabolóide.

A Descida Gradiente

Como vimos acima, funções quadráticas possuem essa formato de tigela, que chamamos de parabolóide. Olhando para a figura é fácil ver que o mínimo dessa função fica lá embaixo, no fundo da tigela, e exatamente pra lá que a descida gradiente vai nos levar.

A descida gradiente é um método simples, mas muito versátil, para resolver problemas de minimização. Em matemática, gradiente é um vetor (uma espécie de seta) que aponta para a direção de maior variação de uma função. Assim, a descida gradiente é um método que vai usar a direção apontada pelo gradiente para ir ladeira abaixo até encontrar um mínimo. É como se o gráfico da função fosse uma rampa e o método da descida gradiente colocasse no nosso pé um skate, nos fazendo deslizar até lá embaixo.

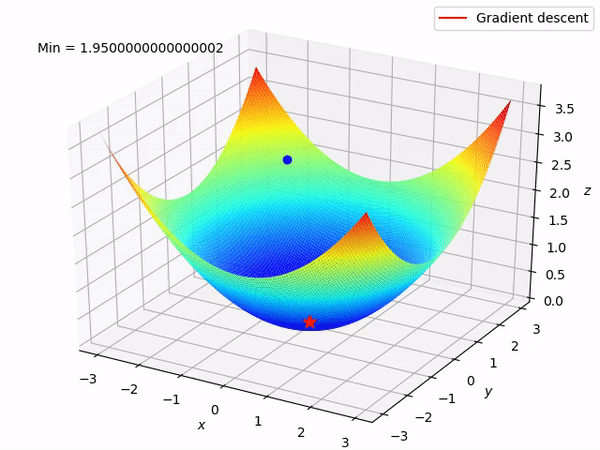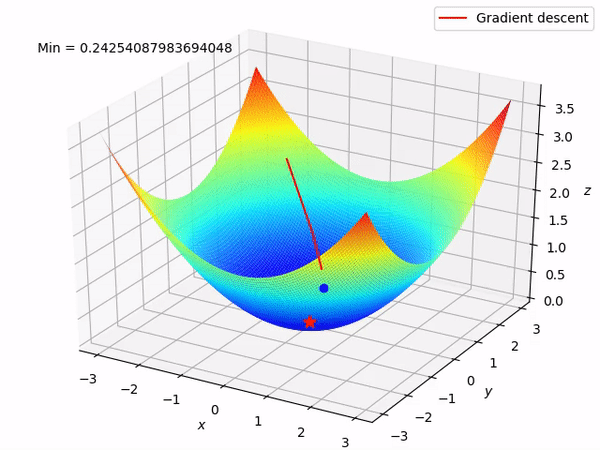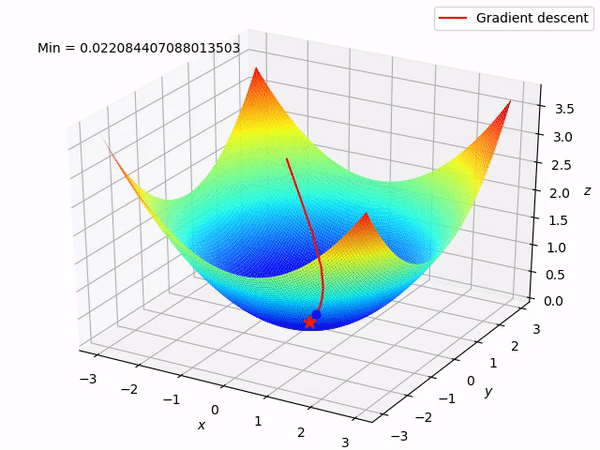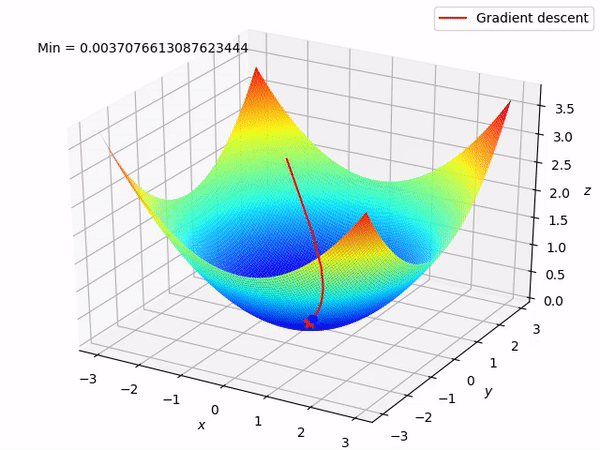
A trajetória ladeira abaixo de uma descida gradiente.

A velocidade com a qual vamos andar na direção do gradiente é chamada de taxa de aprendizado e, geralmente, ela é um valor fixo entre 0 e 1. O segredo desse método é escolher uma boa taxa de aprendizado, senão nós podemos acabar chegando lá embaixo rápido demais e acabar subindo a parede do outro lado, demorando mais pra chegar no fundo ou, até mesmo, ficar pra sempre subindo e descendo pelo gráfico, sem nunca convergir.

Nas fórmulas que vou usar na minha implementação, a taxa de aprendizado será a variável alpha (α). E falando em implementação, vamos colocar a mão na massa e ver como a descida gradiente funciona na prática!

Botando a mão na massa

Antes de começar, precisamos de um problema para resolver. Pra isso, eu fui no Kaggle para procurar datasets adequados para a aplicação de regressão e acabei encontrando um dataset muito legal de carros usados no Reino Unido, organizados por marca e modelo. Eu acabei escolhendo o arquivo que continha informações de Ford Focus colocados para revenda, um carro comum de se ver aqui pelo Brasil também.

O dataset do Kaggle que escolhi.

O primeiro passo foi retirar do dataset completo, com mais de 5000 entradas, um subconjunto para usarmos no treino do nosso modelo. Eu usei funções de índice na matriz que importei no Octave para extrair uma amostra aleatória com 500 entradas. O passo seguinte, então, foi ler essa amostra e preparar os dados para serem usados na descida gradiente.
 

data = csvread('data/focusSample.csv'); % Le o arquivo com dados
data = sortrows(data,2); % Ordena os dados pela milhagem
prices = data(:,1); % Precos ficam na primeira coluna
mileage = data(:,2); % Milhagem fica na segunda coluna

 
Para visualizar os dados usamos a função scatter, que desenha uma bolinha para cada entrada da nossa amostra. O resultado deve ser parecido com esse:

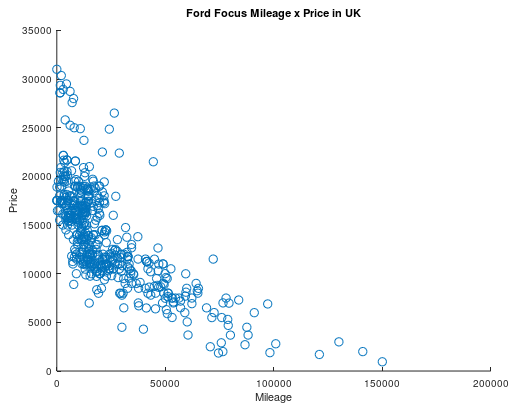
Cada bolinha é uma entrada do nosso dataset, estamos mostrando o preço em função da milhagem.

Com isso, confirmamos nossa hipótese de que carros com maior milhagem são, em geral, mais baratos. Agora vamos preparar os dados para usá-los de entrada na descida gradiente. Para que o algoritmo tenha uma melhor performance, é ideal que as duas variáveis estejam na mesma faixa e, por isso, nós vamos normalizar as variáveis. Normalizar nada mais é do que dividir todas entradas da amostra pelo valor máximo dela, fazendo com que só tenhamos valores entre 0 e 1. Para conseguir recuperar os valores originais nós também salvamos o valor dos máximos.
 

maxPrices = max(prices);
maxMileage = max(mileage);
prices = prices/maxPrices; % Normaliza os precos
mileage = mileage/maxMileage; % Normaliza a milhagem

 
Com os dados prontos, vamos agora nos concentrar na implementação da descida gradiente. Antes de partir para o código, é importante relembrar a forma da equação da reta:

Nela temos nossa variável dependente, y, a variável independente, x, e os nossos coeficientes, os θ (essa é a letra grega theta). No nosso problema, y é o preço do carro, que queremos estimar a partir da milhagem x, e usamos os coeficientes θ para adequar a reta na amostra de treinamento. Por fim, vamos aplicar a descida gradiente nos θ e, para poder usar operações matriciais para fazer toda essa operação, vamos preparar os dados da seguinte maneira:
 

alpha = 0.1; % Nossa taxa de aprendizado
X = [ones(length(mileage), 1), mileage]; % matriz X, com [1, x]
y = prices; % vetor alvo, com os preços da amostra de treino
theta = zeros(2, 1); % vamos usar 0 como chute inicial para theta

 
Note que criamos uma matriz X com a primeira coluna só de 1 e a segunda com os dados da milhagem. Isso é porque, na equação da reta, temos 1 multiplicando θ₀ e os valores de x, a milhagem, multiplicando θ₁. Esse é um padrão que pode ser estendido para um polinômio de qualquer grau. Por exemplo, o código abaixo iria preparar uma função de segundo grau para ser input na descida gradiente:

X = [ones(length(mileage), 1), mileage, mileage.^2]; % agora com x^2
y = prices;
theta = zeros(3, 1); % agora temos 3 theta

Finalmente, vamos implementar nossa descida gradiente! Primeiro vamos fazer a função de custo, que vai estimar o erro da nossa aproximação a cada passo, que me ajudou bastante na hora da investigar erros na preparação dos dados ou na própria implementação do modelo. Essa função é a soma dos erros quadráticos, que discutimos lá em cima:

Com isso em mãos, a minha implementação da descida gradiente ficou assim:

Note que eu estou salvando, e retornando, o histórico dos θ e dos erros J. Isso é para que possamos, como eu disse antes, investigar problemas e também para visualizar a evolução do nosso modelo! Então vamos chamar essa função e ver como ficou nossa reta:

[theta, cost_history, theta_history] = gradientDescent(X, y, theta, alpha, num_iters);
scatter(mileage*maxMileage,prices*maxPrices)
hold on
plot(X(:,2)*maxMileage,X*theta*maxPrices)
hold off

Ao executar esse código acima, o gráfico com os dados de treino e o modelo gerado vai aparecer na sua tela. Ele deve ser mais ou menos assim:

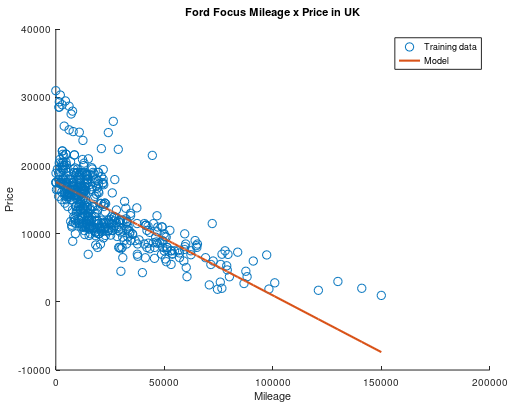
Nada mal para nosso primeiro modelo, não é?

Apesar de não ter ficado ruim, nosso modelo recomenda valores de venda negativos para carros que rodaram mais de 100 mil milhas, e isso não faz muito sentido, não é mesmo? No final, o erro quadrático médio do nosso modelo normalizado ficou em 0.026, que está longe de ser ideal, mas não chega a ser ruim para modelos desse tipo.

O que ficou claro aqui é que uma reta não era uma boa escolha e, desde o começo, notei que o formato dos dados se parecia mais com uma parábola ou função exponencial. Como essa implementação foi pensada para ser geral para polinômios de qualquer grau, eu a modifiquei para treinar um modelo com um polinômio de segundo grau. O resultado então foi esse:

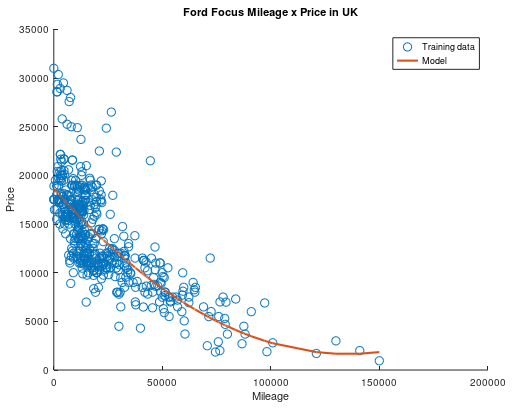
Parece bem melhor, não é mesmo?

Apesar do modelo quadrático se encaixar muito melhor na nos nossos dados de treino, o erro continua em 0.026 no dataset completo. Isso pode acontecer por diversos motivos, dentre eles a escolha da taxa de aprendizado ou da amostra de treino, e este é um assunto que renderia uma postagem só pra ele! Enquanto eu ainda aprendo sobre como melhorar nossos modelos, vamos apreciar a evolução do nosso modelo durante seu treinamento!

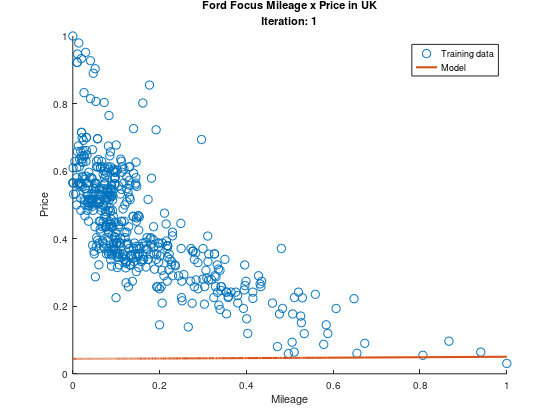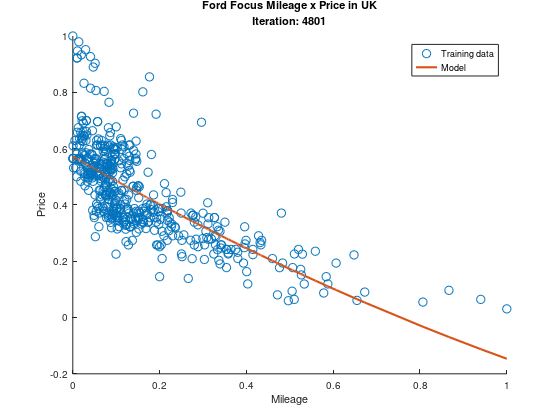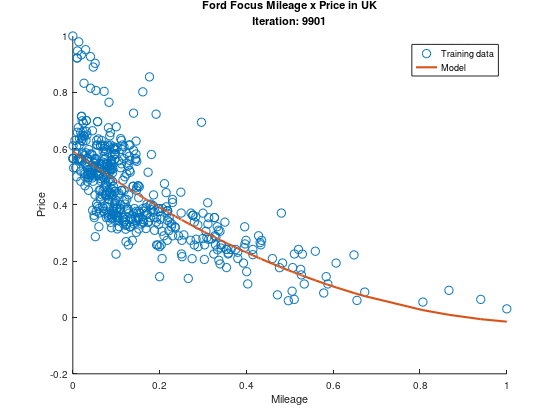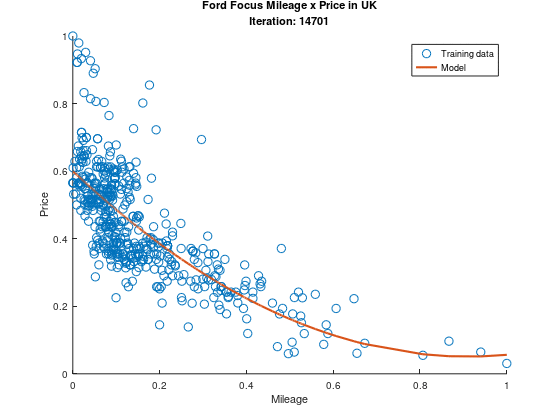
É tão bonitinho, não é?

Bom pessoal, por hoje era só. Espero que tenham gostado da minha jornada até a construção do meu primeiro modelo de machine learning e, quem sabe, vocês também tenha aprendido alguma coisa comigo! Muito do que aprendi para construir esse post foi no curso de machine learning de Andrew Ng, então não deixe de conferir que vale muito a pena.

Por fim, fiquem ligados aqui no blog porque também quero dividir com vocês a minha jornada para implementar um algoritmo de aprendizado não supervisionado! Até lá, deixo para vocês o desafio de conseguir erros menores que o dos modelos que apresentei aqui e, se conseguirem, me mandem um e-mail ou mensagem contando como foi. Todo o código que usei está disponível no meu GitHub, e vou deixar o link para o repositório aqui!

Até mais pessoal!